|
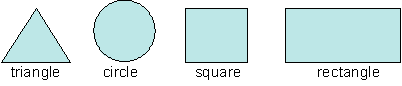
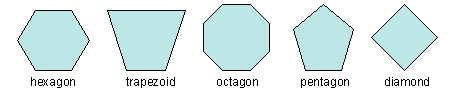
Basic Shapes |
|
|
|
|
 acute angle |
An acute angle is an angle whose measure is greater than 0° and less than 90º. |
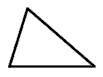 acute triangle |
An acute triangle is a triangle that has three acute angles. |
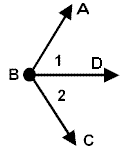
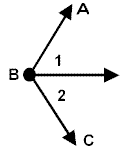 <1 and <2 are adjacent <1 and <ABC are not adjacent |
Adjacent angles share a common vertex, a common side and no common interior points (they do not overlap). |
 Altitude for an obtuse triangle. |
The altitude of a triangle is a line segment extending from any vertex of a triangle perpendicular to the line containing the opposite side. |
 |
An angle
bisector is a ray whose endpoint is the vertex of the angle
and which divides the angle into two congruent angles.
|
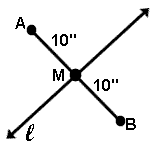 |
Bisector of a line segment is any line (or subset of a line) that intersects the segment at its midpoint. |
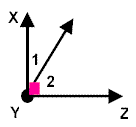 <1 and <2 are complementary |
Complementary angles are two angles the sum of whose measures is 90º. (Complementary angles need not be adjacent angles.) |
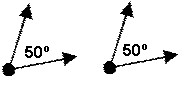 congruent angles |
Congruent angles are angles of the same measure. |
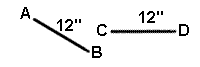 |
Congruent segments are segments of the same length (measure). |
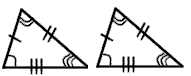 congruent triangles |
Congruent triangles are triangles whose corresponding angles and sides are congruent. (They are exactly the same size and shape.) |
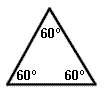 equiangular triangle |
An equiangular triangle is a triangle which has three congruent angles. |
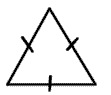 equilateral triangle |
An equilateral triangle is a triangle with three congruent sides. |
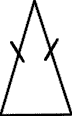 isosceles triangle |
An isosceles triangle is a triangle with two congruent sides. |
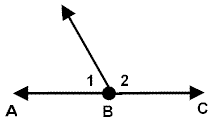 linear pair |
A linear pair of angles are adjacent angles whose non-common sides are opposite rays (form a straight line). The sum of the measures of the angles in a linear pair is 180º. Unlike supplementary angles, a linear pair MUST be two adjacent angles. |
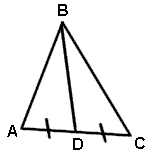 |
The median of a triangle is a line segment extending from any vertex of a triangle to the midpoint of the opposite side. |
 |
Midpoint of a line segment is the point on that line segment that divides the segment two congruent segments. |
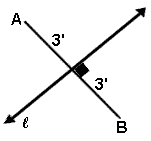 |
The perpendicular bisector of a segment is a line (or subset of a line) that bisects the segment and is perpendicular to the segment. |
 obtuse angle |
An obtuse angle is an angle whose measure is greater than 90º and less than 180º. |
 obtuse triangle |
An obtuse triangle is a triangle which contains one obtuse angle. |
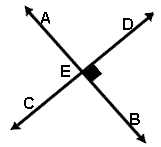 |
Perpendicular lines are two lines which intersect to form right angles. |
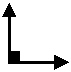 right angle |
A right angle is an angle whose measure is 90º. |
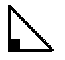 right triangle |
A right triangle is a triangle containing one right angle. |
 scalene triangle |
A scalene triangle is a triangle with no congruent sides. |
|
straight angle |
A straight angle is an angle whose measure is 180º. |
 <1 and <2 are supplementary |
Supplementary angles are two angles the sum of whose measures is 180º. (Supplementary angles need not be adjacent.) |
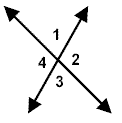 <1 and <3 are vertical angles <2 and <4 are vertical angles |
Vertical angles are two nonadjacent angles formed by two intersecting lines. |
| Form of equation: | Formula: | ||
| Standard Form | ax + by = c | ||
| Slope Intercept Form/ Y Intercept Form | y = mx + b | m = slope b = y intercept | |
| X Intercept Form | x = (y - b)/m | b = y intercept m = slope | |
| Point-Slope Form | y - y1 = m(x - x1) | (x1,y1) m = slope | |

Copyright © Since 1999 - NallPro® All rights reserved.